摘  要：为了更好的的分析各种控制系统的性能和评价不同控制算法的效果，文中介绍了一种通用的锅炉非线性动态模型。通过对500 MW汽轮发电机组上的两个扰动实验的讨论分析，解决了实际锅炉蓄热系数、磨煤机动态和水冷壁动态的求取问题。该文根据燃料量扰动试验中的主蒸汽流量D_t和锅炉的蓄热系数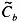与汽包压力P_d的微分的乘积构造出热量信号D_q，替代锅炉总有效吸热量，以求取磨煤机动态和水冷壁动态模型的传递函数，有效地解决了很难通过传感器准确测量的锅炉总有效吸热量问题。将500 MW汽轮发电机组的实际参数和实验计算结果代入模型中，建立起实际500 MW汽轮发电机组的仿真模型。与实际机组的扰动试验数据进行仿真对比，所构造的锅炉模型与实际的压力输出吻合得很好，验证了模型的有效性和正确性。
    关键词：锅炉；动态模型；热量信号；扰动实验

1 引言
    分析锅炉动态特性，构建复现性较好的锅炉动态模型具有重要的意义。首先，一个具有良好复现实际运行机组特性的动态模型能够更好地用于分析各种控制系统的性能；其次，可以建立统一的仿真平台用于评价不同算法设计的控制器的效果。
    近年来较多的研究集中在构造一种通用的非线性动态仿真模型上。1991年F. P. De Mello^[1]  给出了一个通用的大型单元机组的协调控制系统非线性模型，该模型是通过热力学分析构造的。2000年Åström-Bell^[2]介绍了一种详细的汽包锅炉非线性动态模型，描述了复杂的锅炉动态性能，该模型不便之处是很难找到这些所需参数。C.Liu 于2001年描述了一个300MW单元机组的锅炉非线性动态仿真模型^[3]，该模型是通过详尽的热力学分析建立的，但不易于控制器的设计。文[4]曾探讨过一种充分考虑系统非线性特性的汽包锅炉动态模型，并给出了求取动态模型未定参数的方法。
    本文通过扰动实验对500 MW的机组动态特性进行分析，构建出一个实际500 MW机组的动态非线性模型。机组建模对象为山西神头二电厂500 MW的汽轮发电机组，其额定主蒸汽流量D_te为1650 t/h，额定汽包压力P_de为18.97 Mpa，额定主蒸汽压力P_te为16.18 Mpa。
2  锅炉核心模型
    汽包锅炉单元机组是一个复杂的多变量系统，一般可简化为一个具有双输入双输出的对象。其中机组的输出功率和机前压力为被控量；主汽门调节阀开度和燃料量为控制量。
    图1是锅炉的核心模型^[4]，各系数含义为：K₁为汽包的蓄热系数C_d的倒数；K₃为主蒸汽管道的蓄热系数C_t的倒数；K₂，K₄，K₅，K₆为内部系数，用于仿真模型的内部平衡。机组汽包压力的额定参数为P_de，设置为积分器1的初始值；主蒸汽压力的额定参数为P_te，设置为积分器2的初始值；主蒸汽流量的额定参数为D_te；假设锅炉的有效吸热量D_q和汽轮机阀门开度指令m均已标幺化，则D_q和m 可描述为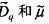。这些参数的求取方法参见文 [1]。

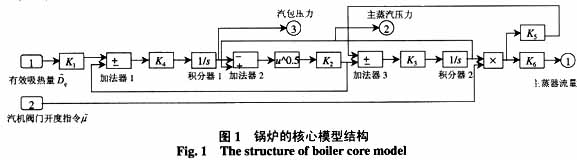
    该模型体现了机组的本质特征，即两个能量平衡关系和两个非线性关系：
   （1）锅炉动态模型的两种相关的能量平衡关系：
    1) 汽包压力P_d反映了锅炉的有效吸热量D_q和汽包出口蒸汽发热量D_k的平衡。汽包蓄热系数C_d反映了汽包蓄能的大小；
    2) 主蒸汽压力P_t反映了汽包出口蒸汽发热量D_k与主蒸汽发热量D_t的平衡。主蒸汽管道蓄热系数C_t反映了主蒸汽管道蓄能的大小。
   （2）锅炉动态过程中存在的非线性特征主要反映在两个方面：
    1）汽包压力P_d和主蒸汽压力P_t的压力降同汽包出口蒸汽流量D_k之间存在着平方根关系；
    2）主蒸汽流量D_t同汽轮机调节阀通流面积F和主蒸汽压力P_t的乘积成比例关系。
    为得到K₁和K₃，要保持燃烧率不变，作汽轮机阀门开度扰动试验。试验中，虽然主蒸汽流量和汽包压力都在变，但是热量信号不应改变。锅炉总蓄热系数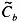可通过下列方程得到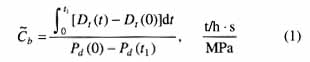

    上式求出的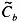是具有工程量纲意义上的数。要将上式求出的总蓄热系数转换为数学模型图1中的系数，一般为

式中  C_b为锅炉总蓄热时间常数。
    理论分析和工程实践已经证明，汽包的蓄热C_d通常占90%，主蒸汽管道的蓄热C_t通常占10%。
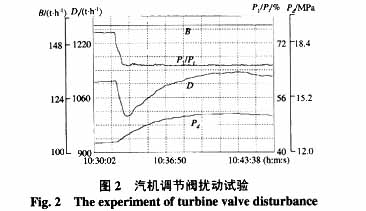
    图2为在山西神头二电厂500 MW机组上做的汽机调节阀扰动试验，其目的是：根据采集到的数据曲线，求取锅炉的蓄热系数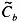。由图2可见，锅炉的总燃料量曲线B在实验的整个过程保持不变，另一曲线用P₁ / P_t代表阀门开度（P₁为汽轮机调速级压力），当汽轮机调节门作向下的阶跃扰动时，开度值由75.16%变到65.53%，降低了9.63%。同时记录主蒸汽流量D_t和汽包压力P_d的变化曲线，然后根据式(1)和(2)计算蓄热系数，得到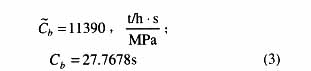

    根据图1锅炉核心模型可写出它的非线性状态方程组如下：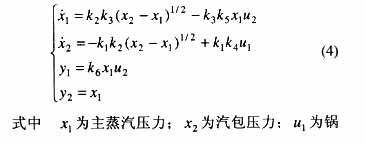

炉有效吸热量；u₂为汽机调节阀门开度；y₁为主蒸汽流量；y₂也为主蒸汽压力。
    式(4)中的参数可由式(3)和文[4]中介绍的方法求得

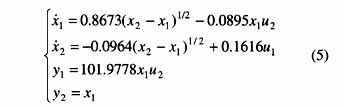
3  磨煤机动态及水冷壁动态模型
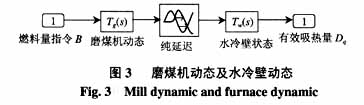
    为了更加完整地复现锅炉对象，需要导出锅炉有效吸热量的动态模型。通常，炉内燃烧与传热过程可简化为磨煤机动态和水冷壁动态两部分，见图3。其传递函数模型可表示为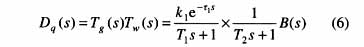

式中  B为进入炉膛的燃料量；D_q为锅炉总有效吸热量；τ₁、T₁、T₂和k₁为传递函数系数，可通过计算或试验求得。

为了求取上述对象的数学模型，需要测量锅炉总有效吸热量，而锅炉总有效吸热量很难通过传感器准确测量。为此，构造出以热量信号替代锅炉总有效吸热量的方法，热量信号描述为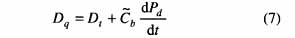

式中  D_t为主蒸汽流量，代表进入汽机的能量，即锅炉能量的输出；汽包压力P_d的微分代表了锅炉蓄热量的变化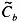；为锅炉蓄热系数。
    热量信号提供了一种在稳态和动态工况下都适合的反映锅炉燃料量变化测量方法。 
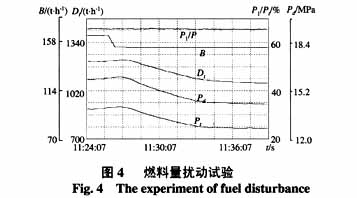
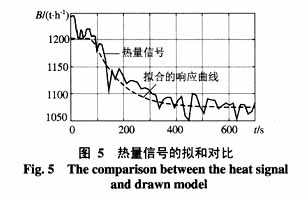
    图4为在山西神头二电厂500 MW机组上做的燃料量扰动试验，其目的是：根据试验数据，构造出热量信号。在工况点：D_t=1202.438 t/h，P_t=14.085 MPa，P_b=15.554 MPa，总燃料量B由164.55 t/h变化为153.42 t/h。根据式(7)，可得如图5所示的热量信号响应曲线。

    式(6)确定了热量信号对燃料量的数学模型结构。采用面积法辨识该模型^[5]，其传递函数为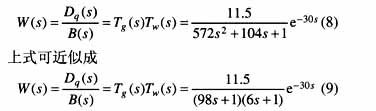

    将有效吸热量的动态模型分为两部分，由理论实践可知磨煤机动态决定其主要的惯性迟延，因此，磨煤机动态模型为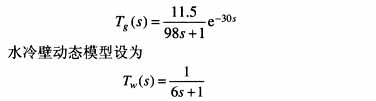

    在相同的工况点，将图4中实际的燃料量信号B作为有效吸热量动态模型的输入，由此得出拟合的有效吸热量响应曲线。由图5可见，拟和的响应曲线与实际的热量信号曲线基本吻合，部分验证了所求取的磨煤机动态和水冷壁动态模型的正确性。

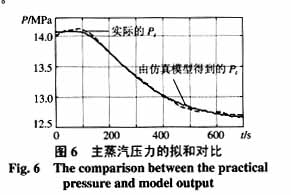
    将热量信号标幺化，即传递函数式(9)的比例系数除以额定吸热量（1650 t/h），比例系数变为0.007。将磨煤机动态与锅炉核心非线性模型连接起来，就组成一个完整的锅炉动态模型。将锅炉的核心非线性模型设置为实际的工作点（K=0.7287，μ=0.8371，积分器1的初始值设置为15.554，积分器2的初始值设置为14.085），再将实际的燃料量指令的变化量引入仿真模型，由此得出的主蒸汽压力P_t响应曲线。由图6可以看出两者吻合得很好，这可以证明在此工作点下，所求出的磨煤机动态和水冷壁动态数学模型的有效性。

  

4  结论
    本文构造出一种通用的锅炉非线性动态模型。通过对神头二电厂500 MW汽轮发电机组上的两个扰动试验的讨论分析，解决了实际锅炉蓄热系数的求取问题。文中采用热量信号替代锅炉总有效吸热量，以求取磨煤机动态和水冷壁动态模型的传递函数，解决了锅炉总有效吸热量很难准确通过传感器测量的问题。将500 MW汽轮发电机组的实际参数和实验计算结果代入仿真模型中，方便地建立起实际500 MW汽轮发电机组的仿真模型。与实际机组的扰动试验数据进行对比，所构造的500 MW锅炉动态模型与实际的压力输出吻合得很好，验证了模型的有效性和正确性。由于时间和篇幅原因，文中验证工作并不完全，需要做进一步的仿真验证，即在锅炉尽可能多的工作点验证模型的有效性，这将是我们下一步要做的研究工作的重点。另外，关于主蒸汽管道压力降的非线性关系，可以通过数值分析、多项式拟合等方法来加以简化。

参考文献

[1]   Mello F P De. Boiler models for system performance studies[J]. IEEE Transactions on Power Systems, 1991,6(1)：66-74.
[2]  Åström  K J, Bell R D. Drum-boiler dynamics[J]. Automatica, 2000,36：363-378.
[3]  Liu Changliang , Liu Jizhen. Nonlinear boiler model of 300MW power unit for system dynamic performance studies[A]. 2001 IEEE International Symposium on Industrial Electronics Proceedings[C], Pusan, Korea, 2001,1296-1300.
[4]  曾德良，刘吉臻（Zeng Deliang, Liu Jizhen）.汽包锅炉的动态模型结构与负荷/压力增量预测模型（Drum boiler dynamic model and load/pressure increment predict model）[J].中国电机工程学报（Proceedings of the CSEE）,2000,20(12)：75-79.
[5]   胡德文.非线性与多变量系统相关辨识 [M]. 长沙：国防科技大学出版社，1992